What’s Happening

EmetteJep:

Thanks for your comment. I hope to post more but I am not sure when that will be. I have more insect photos waiting in the wings.

Lately I have been experimenting with efficient twig-fueled cooking stoves. I am very pleased with the results. Anyone interested can find what I did by doing a search on “rocket stoves”.

I have also been experimenting with regenerative radios, trying to find the one that uses the least power and fewest number of active devices (read: “transistors”) yet performs with sensitivity, selectivity, stability and covering a wide tuning range that includes short wave as well as AM broadcast. Someday I may publish my results. So far, it seems to me that three transistors are the minimum needed for a practical radio. I have been able to get one to run a long time on the power left in a battery that, for other purposes, is essentially dead.

From my organic garden I have been eating strawberries. Also: peppermint, curly dock, dandelion leaves, wild grape twigs and leaves, lambsquarters, winter savory, sorrel, garlic chives, common chives, wild lettuce and green onions. I typically collect a bowl full of an assortment of the above, wash it, chop it up fine, mix it with a bit of mayo, and eat it with biscuits, along with a tea from roasted dandelion roots.

I also love poke. It is very tender and has a delicate flavor. I do not include it in the above mix because it needs to be boiled twice before eating (or so I have heard; being one never to doubt authority, I always boil my poke twice).

I have a potato plant I transplanted when it volunteered in an inconvenient spot. Sweet potato slips are sprouting in the kitchen window. I also have carrots raising their heads in the garden. Carrots are all I deliberately started from seed this year (so far). They are slow growers, but I am faithfully keeping them watered and weeded.

I recently dumped a good bit of compost on the raised bed garden. The compost came from worm bins kept in the basement and an outside compost pile.

I still collect rainwater and filter it with a slow sand filter. I use the filtered water to hydrate the basement worm bins. I use unfiltered water to hydrate the outside bins and keep the seedlings from wilting.

I am still eating last years’ sour kraut from a jar in the refrigerator. It has been several months since I checked what is growing in the crocks kept in the basement. Reluctance to look comes from a little fear about what I might find.

I have not baked sour-dough bread for a while but I know how easy it is to create another starter from whole wheat flower should I ever need to.

I recently learned that the secret to soft biscuits is adding sugar to the dough.

I have not used the solar oven yet this year, mostly due to a sparsity of sunny days. It looks like summer is about to put an end to our rainy season soon, though.

It has been a good spring for wild mushrooms, but I have not found any that I could identify well enough to eat.

I am still convinced we need to take a serious look at true socialism. Obamanomics, the hysteria of media lick-spittles aside, is not socialism.

I might take up oil painting again soon. I did that a bit a very long time ago but have some new ideas about mixing paint that I want to try.

As you see, I keep very busy. Blogging frequently sits on the back burner. Thanks, again, for your interest.

Curlydock

First Multi-Mirror Solar Oven Simulations

by Curlydock
Nov 27, 2007

Results published in previous posts increased confidence in my solar oven simulation program. Those tests were confined to the single-mirror configuration. By keeping things simple, results were intuitively judged. Now it gets more interesting as we encounter kaleidoscopic multi-mirror configurations with results that may challenge intuition but that are, nevertheless, we hope, still accurate.

The number of variables that define the problem make closed form expression prohibitive, at least for me. Thus, my use of simulation.

HERE IS A LIST OF THOSE VARIABLES:

The oven seems simple enough in that it is composed of two sets of hinged mirrors and a sphere called a “bounding sphere” that stands for the oven cavity. The oven cavity is the part of the oven that gets hot enough to cook food. It is constructed like a small green house, but we need not concern ourself with those details.

The bounding sphere is all we need to know about the oven cavity. The center of the sphere gives the CAVITY LOCATION in EXTENSION and ELEVATION from the “origin”, the lowest point on the vertical R1-R2 hinge. The cavity location is always in the bisecting plane of the oven’s bilateral symmetry.

The radius of that sphere gives the SIZE OF THE CAVITY. Now, to make results easier to compare across simulations, I have normalized all units of distance to the diameter of the oven cavity. So, instead of inches, feet, meters, etc, all lengths are in units of cavity diameters.

I have named the four mirrors of concern: R1, R2, R3 and R4. Hinged on a vertical axis are R1 and R2. R3 and R4 are hinged horizontally. So, we have the two angles: R1–R2 ANGLE and R3–R4 ANGLE.

We will also be concerned with where the sun is in respect to our oven, so we have: SOLAR ALTITUDE ANGLE or elevation; zero degrees on horizon and 90.0 degrees at zenith, and SOLAR AZIMUTH ANGLE. In all runs I presently contemplate, the azimuth will not change, confining the sun to the plane that bisects the symmetry of the oven.

We also have to be concerned with R1 WIDTH and R1 HEIGHT. R2 is always identical to R1 in width and height.

Since R3 and R4 are hinged horizontally, it is confusing to speak of their width and height, so I define the dimension R4 RATIO, the length of the horizontal hinge, as a portion of the opening of R1-R2.

R3 is always parallel to, or in the plane of, the horizon. R1-R2 sits on R3 like an open book with the bottom two corners on the axis of the R3-R4 hinge. Because of this configuration, the reflective part of R3 will always be a triangle with size and shape determined by the width of R1, R2 and the R1-R2 angle. The other mirrors are always square or rectangular.

R4 EXTENSION is how far R4 extends from the horizontal hinge.

Also an input variable is the QUANTITY OF REFLECTIVE PLANES. I can consider four possibilities: R3 only; R1 and R2; R1, R2 and R3; as well as all four mirrors.

I think that about covers the input variables. So far I have not concerned myself with losses based on reflective angles, surface imperfections, convection, conduction, mass, re-radiation, transmission distances, imperfect insulation, etc.

OUTPUT

What we get for output is the amount of idealized SOLAR FLUX GAIN on the oven cavity over what the cavity would have gotten directly from the sun without any concentration. This is not a temperature; it is a ratio. The minimum value will always be 1.0 unless the cavity is in shadow or blocked from direct rays, where the value could fall to zero. The maximum value depends on all the inputs.

Because of the large quantity of possible combinations of input variables, I must find a way to lock some of them down so they can be temporarily ignored. That will simplify the problem and help us make sense of where we are in our journey to the “perfect” design. I do not know if there can ever be a proof that a particular design is the best possible one. There might always be a combination of inputs hitherto unconsidered that will yield a greater flux gain than what we thought was the best. If there is such a proof, a bigger brain than my own will need to find it.

That is why I am willing to share my program listing with anyone who is interested and who agrees to keep my program or any derived from it in the public domain, not for profit.

I am also willing to do runs for others who would like to see particular results of inputs meaningful to them. Perhaps they have built an oven or two and want to see what the simulation says about comparative performance. If you are interested, just leave your request in the comments section and I may publish my response or run results in a future post.

Next, some multi-mirror runs:

For the time being I will keep R1-R2 angle at 60.0 degrees. The decision is arbitrarily based on the fact that an oven I built uses that angle. In the long run, there may be a better angle.

Also, for now I keep the width of R1 at 4.0 cavity diameters. I do that because prior runs with R3-only seemed to result in 4.0 as the optimum size for the side of R3, given the R1-R2 angle = 60.0 degrees. The length of a side of R3 is the same as the width of R1 (and R2). Lastly, to start, I make the height of R1 equal to its width.

Chart “nov1029a” shows the effect of cavity extension on flux gain where only R1 and R2 are in play. For these inputs, the best value seems to be 1.4, but it depends on the angle of the sun. By this chart, for sun angles higher than about 40.0 degrees we might want to make the cavity extension less than 1.4 cavity diameters.

Next, keeping cavity extension at 1.4 and everything else the same, we do four runs, one for each of four different heights of R1-R2. That results in chart “nov1030” where
red (1) = 4.0
green (2) = 6.0
blue (3) = 8.0
black (4) = 10.0
cavity diameters.

We see gains increasing at higher sun angles as the height of R1-R2 increases. The gain increment decreases so returns are diminishing. At this point I will make the compromise of R1-R2 height = 6.0 and keep that for the next set of runs.

I cannot resist the temptation to add more mirrors at this point. Chart “nov1032” run (1) is a repeat of “nov1030” run (2), for reference. It looks different because the vertical axis of the chart is re-calibrated to cover higher gains.

Note the gain still peaks at about 6.0. That gain makes sense when you consider that two mirrors at a 60.0 degree angle would allow the sun to see six images of the cavity. Run (1) is only with R1 and R2 in play.

For run (2) I merely add reflector R3 to the play, and the results show a significant increase in gain. If we consider that R3 would double 6 images to 12, the gain seen of about 9.0 makes sense, considering some of the images will be partially obscured.

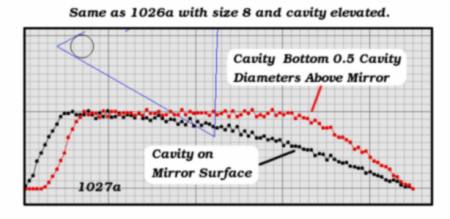
Now we take a lesson from a prior post when we were testing with only R3 and learned that it is best to elevate the cavity somewhat over R3. We do just that in run (3) and see that the gain is even closer to 12.0. Supposedly, the reason is that the images are less obscured when the cavity is elevated.

In run (4) I put R4 in play and made R4 the same size and shape of R1 and R2. It is a handy size if the oven is collapsible and you stack the reflectors for storage. The solar flux gain reached 14.0. One might worry that the simulation is malfunctioning because the flux gain is below 1.0 for very low angles of the sun. More thought reveals that at these low solar angles the cavity and lower part of the oven are in the shadow of R4, so one’s confidence in the program rebounds.

Is this the best design? I doubt it. Only more testing can tell, I guess. At least, it is a benchmark for measuring more attempts.

In a future post I can make the input variables conform to the oven I have actually constructed and see what the simulation says. I will be able to compare a real oven with this benchmark and tell what changes might make it better or worse without getting my hands dirty (not meaning to disparage getting one’s hands dirty).

Last Single-Mirror Solar Oven Simulation Test

by Curlydock
Nov 24, 2007

In my previous couple of posts I showed some of the results of tests of a program I wrote to simulate what I call a “kaleidoscopic” type solar oven. In earlier posts I detail the actual oven I use to bake bread. I wanted to see how to build a better oven of this type, so I wrote the simulation for ray-tracing various reflector sizes, shapes, quantities and configurations.

This post will cover what I hope is the last of the one-reflector tests. I wish to begin tests of two-mirror simulations in the next post.

Graph “nov1026a” shows the results of five runs with a single equilateral triangular reflector in the plane of the horizon. That reflector I frequently refer to as “R3”. Five sweeps of the sun from zero degrees (horizon) to 90 degrees (zenith) are shown, one sweep for each size of R3. The sides are all equal and are measured in cavity diameters. The smallest R3 is 2.0 and the largest is 8.0 cavity diameters on a side. The cavity bounding sphere is represented by the ball that is aways in the corner farthest from the sun when the sun is on the horizon.

Observe that the gain never exceeds 2.0 and never falls below 1.0. This is consistent with my expectations of what happens with only one mirror and increases my confidence in the simulator.

Rule 1026a

Also observe that the increment of improvement in gain decreases as R3 gets larger. Large mirrors increase the gain when the sun is at lower angles but the reflector has to get perhaps impractically large to produce these gains. At solar angles above about 20.0 degrees, it hardly seems worth having a floor reflector larger than 4.0 cavity diameters on a side. This is more than my prejudice up until now, which was that 3.0 cavity diameters on a side was the practical limit. The actual oven I made has only 3.0. So, the next time I build one of these ovens I will probably go with 4.0. It depends on what else we learn when more reflectors are in play.

“Rule 1026a” is, then: the triangular reflector always parallel with the plane of the horizon, that is the one the cavity is above, should be sized to about 4.0 cavity diameters on a side, physical practicality permitting, and probably not less than 3.0.

Now I combine this rule with rule 1010a from the previous post, which said the cavity should be elevated. That results in chart “1027a”:

For this run I kept the mirror sized to 8.0 cavity diameters on a side and elevated the bottom of the cavity from just touching R3 to where the bottom of the cavity is 0.5 cavity diameters over R3. Otherwise the run and chart calibration are the same.

Again, the gain never exceeds 2.0 and never falls below 1.0, which is good.

Also note that elevating the cavity improves gain when the sun is at higher angles. This is consistent with what we learned in the prior post and was to be expected. The simulation still seems to work. For this configuration, with the cavity elevated, the range of sun angles with the maximum gain of 2.0 is much larger.

In a prior post I expressed some doubt about whether the simulation was following the ray trace through an arbitrary number of reflections or breaking off too soon. I later discovered that was indeed a problem. But it only affected simulations of more than one mirror, none of which I had published yet. I fixed the bug and am now confident that I am ready to do multi-mirror tests. In the next post we will see some results using two reflectors. Those reflectors are the ones I have named “R1” and “R2” in prior posts. They are linked by a vertical hinge and open like a book over the plane of R3. R3 will be put aside while we consider only R1 and R2 and will return probably much later when three-mirror tests begin.

More Elementary Tests of a Solar Oven Simulation

by Curlydock

Nov 16, 2007

In the prior post I introduced a test of the simulation using only one plane of the “kaleidoscopic” type solar oven. So far, we have seen the bounding sphere of the oven cavity positioned over one triangular concentrator. That concentrator corresponds to the R3 reflector mentioned in other posts describing an actual oven that I have been using. The R3 reflector is in the plane that appears to be parallel with the earth’s surface and the cavity assembly rests on R3. In later posts we will be considering the effect of the other reflectors: R1, R2 and R4. This post is confined to more implications of the R3 reflector.

Diagrams “nov1007” and “nov1008” illustrate the oven cavity bounding sphere positioned at two different levels over the triangular reflector.

The red dots represent the absorption of a light ray on the surface of the bounding sphere. The blue dots represent rays reflected from the surface of the mirror that do not intercept the cavity. The shadow of the cavity can be seen on the mirror. The other dark spot on the mirror is that portion of the mirror where rays are reflected that do intercept the cavity.

This Test

The present question is how the height above the mirror affects the amount of solar flux gain the cavity will receive as the sun sweeps over an altitude angle from zero degrees on the horizon to 90 degrees at the zenith.

Diagram “nov1010” shows the result of four simulated solar sweeps, one for each of four different heights of the oven cavity above mirror R3.

On Units

Unless otherwise noted in these posts, the units of distance measurement will be cavity diameters. I think that is more interesting and informative than using yards or meters, etc. So, no matter what the radius of the cavity is in feet, centimeters, inches or any other unit, it is always 0.5 in cavity diameters. When the cavity rests on the mirror the center of the cavity will be 0.5 cavity diameters from the surface. The lowest point on the cavity, in that case, will be zero cavity diameters from the mirror.

The triangular mirror, R3, seen in the above illustrations and used in this particular post, is equilateral and 3.0 cavity diameters on a side. The cavity CENTER heights used to generate the data for the chart “nov1010” are 0.5 (red), 1.5 (green), 2.5 (blue) and 3.5 (black) cavity diameters. There is one color coded sun altitude sweep for each cavity placement.

The Solar Sweeps

These “altitude sweeps” are not the natural movements of the sun, so don’t be confused. The sweeps begin at the lowest point on the horizon and end at the highest point in the sky, or the zenith, at 90 degrees. The point on the horizon, zero degrees, where the sweep begins, is always in a vertical plane that bisects an angle of the triangular reflector.

The reason for this type of sweep is to see how the more complicated mirror arrangements respond to different solar angles, all of which keep the sun in the plane that bisects the symmetry of the concentrator arrangement. The purpose was to have a standardized sweep with which to compare different arrangements under any solar angle that might happen no matter what the season, location on the earth, or time of day, given that one could always adjust the oven so the sun is in that bisecting plane. Such an adjustment would not change the fact that R3 is in the plane of the horizon; it would merely rotate R3 in that plane. The tests to see how the simulated oven responds to a natural solar transit will probably be some of the last tests.

Rule 1010a

Now back to chart “nov1010”.

Note that when cavity height is lowest, 0.5, which corresponds to touching the mirror, the gain never reaches the greater levels it does when the cavity is elevated from the mirror. This is the reason for placing the inverted glass bowl underneath the oven cavity assembly, as seen in my prior posts detailing an actual solar oven. The lower bowl elevates the whole assembly a bit. I was never quite sure just how much it should be elevated but now it seems my simulations may help to determine this.

So, Rule 1010a for building kaleidoscopic solar ovens is: elevate the cavity over the mirror that is parallel to the plane of the horizon instead of letting it rest on it.

Next, we see just how much elevation is best. The above graphs suggest that the best cavity elevation will depend on the solar altitude. The angle of the sun is constantly changing; so, if we can figure out a way to easily adjust the cavity elevation about every twenty minutes, that would optimize flux gain at all times. Such a rig might be more complicated than the extra flux gain is worth, however.

Diagram “rule1010a”, seen below, might be used in the design and operation of a one-triangular reflector solar oven with an equilateral shaped mirror three cavity diameters on a side. It probably would not work for baking because the flux gain would never exceed 2.0. It might be useful for proofing bread dough or keeping a plate warm. It might also apply to ovens with more reflectors, but we have to wait to see what more tests produce to be sure.

This diagram allows us to determine the best cavity height above the reflecting plane for any given altitude angle of the sun. I gathered the data for the diagram from repeated runs with the simulation program. That these curves seem to make sense to me reinforces my confidence in the accuracy of the program so far (no guarantee, of course).

The runs show rather broad peaks. That suggests that a particular cavity elevation would work well for a wide range of solar angles without need to re-adjust the height. For that reason, the diagram “rule1010a” shows a region instead of a line. The acceptable region is in yellow-green between two limiting lines. The limiting lines represent the points where the solar flux gain has dropped to 0.9 times the peak value seen in the sweep. The graph seems to indicate that for solar angles below about 25 degrees there is no need to elevate the cavity at all. The flux gain might be very low, but elevating the cavity will not help.

How to Apply Rule 1010a

Here is an example of the use of diagram “rule1010a”:

Suppose the sun is at 70.0 degrees above the horizon. Find 70.0 degrees on the horizontal axis of the chart. Follow the vertical from 70 degrees up until it just reaches the green region (the first limiting line). Follow the horizontal from that point to read the cavity height. That yields about 0.70 cavity diameters.

Continue on the 70.0 degree vertical until the green region just ends (on the other limiting line). Following the horizontal from that point yields about 2.9 cavity diameters.

Therefore, the maximum gain will be when the BOTTOM (not the center) of the cavity is between 0.70 and 2.9 cavity diameters from the surface of mirror R3.

If the cavity is 12.0 inches in diameter then 0.70 cavity diameters represents 0.70 X 12.0 = 8.4 inches. Likewise, 2.9 cavity diameters X 12.0 inches per cavity diameter = 34.8 inches. At these points the gain will be about 9/10 what it would be at the peak.

To find the height corresponding to the actual peak, you can use the average. In this case, the average cavity height is (0.70 + 2.9) / 2.0 = 1.8 cavity diameters, and 1.8 X 12.0 = 21.6 inches.

In the morning and evening hours the sun is not so high and the cavity will not need so much elevation. Even if the cavity elevation is not optimum, the losses will not make the oven useless, it will probably just take a little longer to cook something. Also, when we start adding the other reflectors R1, R2 and R4, the gain will be considerably beyond 2.0, so some small maladjustments will be even less of a problem.